이 질문은 물류 모델이 충분한 지 결정하는 방법에 대한 실제 혼란에서 비롯됩니다. 종속 변수로 형성된 후 2 년 후에 개별 프로젝트 쌍의 상태를 사용하는 모델이 있습니다. 결과는 성공적이거나 (1) 그렇지 않습니다 (0). 쌍 형성시 측정 된 독립 변수가 있습니다. 내 목표는 내가 가정 한 변수가 쌍의 성공에 영향을 미치는지 여부를 테스트하여 다른 잠재적 영향을 제어하는 것입니다. 모형에서 관심 변수는 중요합니다.
의 glm()함수를 사용하여 모델을 추정 했습니다 R. 모델의 품질을 평가하기 위해, 나는 몇 가지 일을 한 것은 : glm()당신에게 제공 residual deviance의 AIC와 BIC기본적에게. 또한 모형의 오차율을 계산하고 구간 화 된 잔차를 플로팅했습니다.
- 완전한 모델은 내가 추정 한 (그리고 완전한 모델에 중첩 된) 다른 모델보다 잔류 편차, AIC 및 BIC가 작기 때문에이 모델이 다른 모델보다 “더 나은”것으로 생각하게됩니다.
- 모델의 오류율은 IMHO ( Gelman and Hill, 2007, pp.99에서와 같이 ) :
error.rate <- mean((predicted>0.5 & y==0) | (predicted<0.5 & y==1)약 20 % 로 상당히 낮습니다 .
여태까지는 그런대로 잘됐다. 그러나 비닝 잔차를 (Gelman과 Hill의 조언에 따라) 플롯하면 많은 빈이 95 % CI를 벗어납니다.
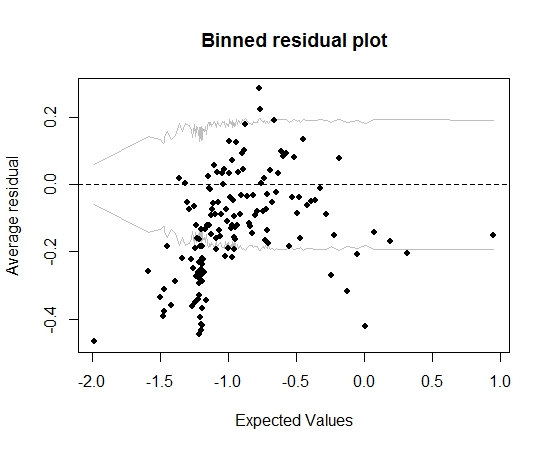
그 음모로 인해 모델에 전혀 잘못된 것이 있다고 생각합니다. 그러면 모델을 버릴까요? 모델이 불완전하다는 것을 인정해야하지만이를 유지하고 관심 변수의 영향을 해석해야합니까? 비닝 잔차 플롯을 실제로 개선하지 않고 변수를 차례로 배제하고 일부 변환을 수행했습니다.
편집하다:
- 현재이 모델에는 12 개의 예측 변수와 5 개의 상호 작용 효과가 있습니다.
- 이 쌍들은 모두 짧은 기간 동안 (단, 엄밀히 말하면, 모두 동시에) 형성되고 많은 프로젝트 (13k)와 많은 개인 (19k)이 형성된다는 점에서 서로 “상대적으로”독립적입니다. ) 따라서 프로젝트의 상당 부분은 한 명의 개인 만 참여합니다 (약 20000 쌍).
답변
분류 정확도 (오류율)는 부적절한 점수 규칙 (가짜 모델에 의해 최적화 됨)으로, 임의적이며 불 연속적이며 조작하기 쉽습니다. 이 상황에서는 필요하지 않습니다.
얼마나 많은 예측 변수가 있는지 말하지 않았습니다. 모델 적합을 평가하는 대신 모델을 적합하게 만들려고합니다. 타협 방법은 상호 작용이 중요하지 않다고 가정하고 회귀 스플라인을 사용하여 연속 예측 변수가 비선형이되도록하는 것입니다. 추정 된 관계를 플로팅합니다. rmsR 의 패키지는이 모든 것을 비교적 쉽게 만듭니다. 자세한 정보는 http://biostat.mc.vanderbilt.edu/rms 를 참조하십시오.
“쌍”과 관찰이 독립적인지 여부를 자세히 설명 할 수 있습니다.
답변
x2